Особенности подготовки интегрированных уроков. Математика и музыка. Целесообразность их проведения

Муниципальное автономное общеобразовательное учреждение

«Средняя общеобразовательная школа №82»

г. Перми

Особенности подготовки интегрированных уроков. Математика и музыка. Целесообразность их проведения

подготовила

учитель математики

Коновалова Лидия Владимировна

г. Пермь

2013

Особенности подготовки интегрированных уроков. Математика и музыка. Целесообразность их проведения.

Математика владеет не только истиной,

но и высшей Красотой — красотой отточенной

и строгой, возвышенно чистой и стремящейся

к подлинному совершенству, которое свойственно

лишь величайшим образам искусства.

В. Рассел

Как известно математика оперирует абстракциями и идеальными объектами, так называемыми идеализациями. Точка, фигура, математическая функция, множество, величина, число — это все математические объекты. С самого своего появления на свет математика оперирует сложной духовной деятельностью человека, так как конструктивная творческая деятельность разума-основы духовного мира, проявляется в создании этих идеализированных объектов и в умении ими устойчиво оперировать.

Какие качества развиваются у детей через занятия математикой? Умение устойчиво оперировать абстракциями и идеальными объектами, следовательно, умения обобщать, абстрагирование связано обобщением. Поэтому математика, великолепный инструмент для развития логического мышления. Одна из сторон духовного мира это интеллект, это развитие.

Проведение и подготовка интегрированных уроков требует большой подготовительной работы, мне, как учителю, необходимо продумать и найти общее не только в содержании, но и в технологии проведения интегрированного урока. Вся работа, обычно, разбивается на два этапа:

1. Первый этап – целеполагание

Все пункты будущего урока обсуждаются совместно с учителями музыки, ИЗО. Сообщается о задуманном учащимся, ребятам предлагается принять участие в проекте плана, возможно, что-то изменить или добавить.

2. Второй этап – выбор оптимальных методов работы.

В течение этого этапа мной и учителями художественно-эстетического цикла выбирается способ подачи материала (игра на инструменте, пение, демонстрация репродукций и т.д.). Параллельно с этим проходит поэтапная работа: поиск материала, дискуссия по каким либо вопросам, оформление, воплощение идей и т.д. Необходимым условием данных уроков является интеграция содержания с предметами художественно-эстетического цикла.

Я считаю, что целесообразность использования интегрированных уроков неоспорима. Во–первых, использование такой методики мотивирует учащихся к изучению математики, повышает их интерес к предмету, дает возможность творческому самовыражению, а значит, дети становятся более активными, с удовольствием идут на сотрудничество с педагогами и одноклассниками.

Во–вторых, подготовка к уроку расширяет кругозор учащихся, учит устанавливать межпредметные связи между дисциплинами, что способствует общему развитию детей, их логическому и аналитическому мышлению. Наконец, сама процедура подготовки и проведения таких уроков предполагает развернутые высказывания детей по заданной теме, следовательно, развиваются речевые умения детей, что является немаловажной задачей при изучении математики.

При регулярном проведении интегрированных уроков учащиеся приобретают:

1) Умения, связанные с развитием интереса:

— анализировать свои интересы,

— сопоставлять свои интересы и возможности.

2) Умение оценивать результаты своей деятельности:

— умение предъявить результаты своей деятельности в виде группового или индивидуального высказывания.

3) умение делать выводы из результатов своей работы:

— объяснить как положительный, так и отрицательный результаты своей работы,

— оценить и осознать практическую ценность для своего дальнейшего развития.

Использование эстетического потенциала на уроках математики и создание интегрированных уроков заинтересовало меня еще и потому, что ощутимо меняется позиция учителя по отношению к ученикам. Их отношения выходят на уровень субъект-субъектных, когда дети становятся не безропотными слушателями прописных истин, а превращаются в активных участников образовательного процесса, заинтересованных в своей реализации и развитии. Кроме того, сам учитель от позиции лектора или контролера переходит к позиции наставника, помощника, где его главной задачей становится консультирование и направление деятельности детей. Несомненно, если педагог желает, чтобы дети работали в атмосфере доверия и сотрудничества, он сам должен начать с доверия к ученикам, как к равноправным участникам общей интересной, творческой и созидательной работы; должен давать возможность для самостоятельной и свободной работы школьников. Таким образом, ребята приобретают не только необходимые знания, умения, навыки, но и развиваются как личность, получая необходимый заряд и навыки для самоопределения во взрослой жизни. Среди основных мотивов, побуждающих учащихся заниматься (интерес к предмету, сознательность, принуждение и т.д.) интерес к предмету, очевидно, самый сильный стимул к учению (я занимаюсь математикой не потому, что преследую какую–то цель, а потому, что сам процесс доставляет мне удовольствие). Занятия при увлечении порождают сильные положительные эмоции и материал «впитывается» легко, без сопротивления. Одним из способов повышения интереса к предмету является необычная подача материала и новизна фактов.

Математика имеет множество великолепных приложений к различным, казалось бы, самым неожиданным аспектам человеческой деятельности, тогда как в школьном учебнике вскользь упоминается лишь в некоторых из них. В результате в сознании учеников со стихийной неизбежностью возникает представление о «сухости», формальном характере математики и оторванности ее от жизни и практики.

Кто же, если не учитель математики, должен навести мосты, соединяющие математику с окружающим миром, показать взаимосвязь естественно-математического цикла с гуманитарным, наполнив уроки конкретными фактами, яркими образами и сделав их содержательнее, разнообразнее, занимательнее.

Целесообразность использования эстетического потенциала на уроках математики.

Прекрасной возможностью связать математику со всем окружающим миром обладает геометрия. Геометрия – это не только раздел математики, это, прежде всего, феномен человеческой культуры, а геометрическое мышление в основе является разновидностью образного, чувственного мышления. Она обладает целым рядом качеств, присущих предметам гуманитарно-эстетического цикла, располагает огромными возможностями для эмоционального и духовного развития. Неслучайно именно уроки геометрии стали связующим звеном между математической наукой и искусством. В качестве иллюстрации, предлагаю несколько фрагментов интегрированных уроков, позволяющих повысить не только познавательный интерес к математике, но воспитывающих математическую и, самое главное, общую культуру учащихся, формируя единую картину мира.

Разговор о многообразных отношениях между математикой и искусством, начнем с музыки, ибо математика, самая абстрактная из наук, и музыка, наиболее отвлеченное из искусств, высшие выразители искусства и науки.

Рассмотрим примеры аспектов, входящих в цель обучения.

1. Учебный аспект

Геометрия – 9, «Правильный пятиугольник»

Помимо задач, предложенных на дом, ребятам необходимо было построить правильный пятиугольник. Поиски построения неограниченны. Ребята предлагали различные способы построения. Одно из построений показалось интересным. Построение правильного пятиугольника с помощью окружностей одного радиуса. Такое построение достаточно сложно, и в то же время своеобразно (целью этого задания явилось умение проработать дополнительную литературу, выбрать оригинальное решение). Вводится понятие «Золотого сечения», сообщается, что ярким примером является правильный пятиугольник или звездчатый пятиугольник, он буквально соткан из пропорций, а прежде всего золотой пропорции. Ученик доказывает теорему о том, что в правильном пятиугольнике каждая диагональ делится другой в отношении «Золотого сечения». Развивается умение сообщить, объяснить, обосновать, убедить, доказать.

А возможно ли, в музыке найти «Золотое сечение»? Звучит музыка Баха. Ребята (музыкальный класс) выполняют несложные вычисления, находят, что «Золотое сечение» приходится на 195-й четверти от начала. Проведя небольшое исследование на слух, понимаем, что вся фантазия представляет собою ряд отделов, подчиненных закону «Золотого сечения». В каждом из отделов золотые сечения почти точно совпадают с кульминационными пунктами (обмен впечатлениями, дискуссия).

2. Познавательный аспект

Геометрия – 8, «Математика и музыка».

Звучит музыка. «Финал 9-й симфонии» Бетховена. Ученик проводит экскурс в историю. Рассказ о жизни Пифагора, о том, как возник институт пифагорейцев, который сделался одновременно и коллегией эстетического воспитания и академией наук. По преданию, сам Пифагор установил законы, на которых основывалась вся пифагорейская теория музыки. Приятные созвучия в музыке получаются лишь в том случае, когда длины струн, издающих звуки, относятся как целые числа, составляющие треугольное число 10 = 1+2+3+4, т.е. 1:2, 2:3, 3:4. Эти интервалы позже получили свое название «октава — 1:2, квинта — 2:3, кварта — 3:4» (данный материал используется как средство обогащения духовного мира личности, приобретение знаний о древней культуре мира).

3. Развивающий аспект

Алгебра – 9, «Квадратичная функция, ее график и свойства».

После построения (по полной схеме графика квадратичной функции), предлагается коллективная творческая работа. С помощью шаблона на индивидуальных карточках построить квадратичные функции с данной областью определения. Ребята замечают, что это не просто графики, а интересные нотки. После этого пронумерованные карточки выстраиваются в ряд. Все замечают, что итогом работы стала строчка из песни «Мы желаем счастья вам». Звучит мелодия. Этот аспект направлен на развитие способности к догадке, приобретение положительных эмоций, развитие умения учиться.

3. Эстетический аспект

Геометрия – 9, «Правильный пятиугольник».

По мнению многих искусствоведов, художников, скульпторов, основные пропорции человеческого тела подчинены законам «Золотого сечения». В построении пропорций человека Леонардо да Винчи исходит, прежде всего, из анализа многочисленных измерений самого человека, из его анатомии. Демонстрируются репродукции, изображающие человека, доказывается присутствие математики. И все-таки самым загадочным, самым притягательным произведением искусства Леонардо да Винчи является портрет Моны Лизы. Портрет долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Демонстрируются шедевры мирового искусства. (Ученики воспринимают красоту через призму математических понятий).

3. Воспитательный аспект

Математика – 6, «Сложение и вычитание дробей с разными знаменателями».

Проблема: на нотном стане записана мелодия песни, нет размера тактовых черт. После прослушивания музыки ребята пытаются решить проблему. Это удается сделать лишь с помощью математических вычислений. Все это бурно обсуждается.

Я считаю, что введение таких интегрированных моментов на уроках, очень полезно. Это необходимо как для развития учащихся, так и для расширения их культурного потенциала. С педагогической и психологической точек зрения использование такой методики очень эффективно, в процессе подготовки к таким урокам происходит:

— создание положительной мотивации к изучению математики, когда в ходе обучения в атмосфере сотрудничества раскрываются потенциальные возможности каждого ребенка,

— развитие творческих возможностей детей,

— создание условий для психологической адаптации к восприятию нового материала,

— активизация стремления к дальнейшему самостоятельному изучению математики.

Все это стимулирует детей к изучению математики, поиску интересных фактов, к дальнейшим достижениям и экспериментам.

Разработка урока геометрии

по теме «Правильный пятиугольник». 9 класс.

Цель урока: Выяснить какими свойствами обладает правильный пятиугольник. Показать значимость его в искусстве, музыке.

Ход урока.

На предыдущих уроках мы говорили с вами о правильных треугольниках, четырехугольниках, шестиугольниках.

— Что мы находили для этих фигур?

— Внутренние углы, стороны, радиусы описанной и вписанной окружностей.

На сегодняшнем уроке рассмотрим еще одну из правильных фигур, это правильный пятиугольник.

— Я думаю, что он покажется вам интересен. Он обладает пока неизвестными для вас свойствами, постараемся их выяснить.

На доске чертеж правильного пятиугольника, вписанная, описанная окружности.

— Вспомним формулы, выражающие стороны, углы, радиус вписанной, описанной окружностей и площадь любого правильного многоугольника. По мере того, как ребята отвечают, на доске появляются формулы.

В тетради вычислите все элементы правильного пятиугольника ( проверка ).

— А теперь, еще раз, вернемся к домашнему заданию. Помимо задач вы должны были построить правильный пятиугольник. Поиски построения не ограничены.

— Как вы это сделали? Предлагали различные способы построения. Одно из построений показалось интересным (по готовому чертежу).

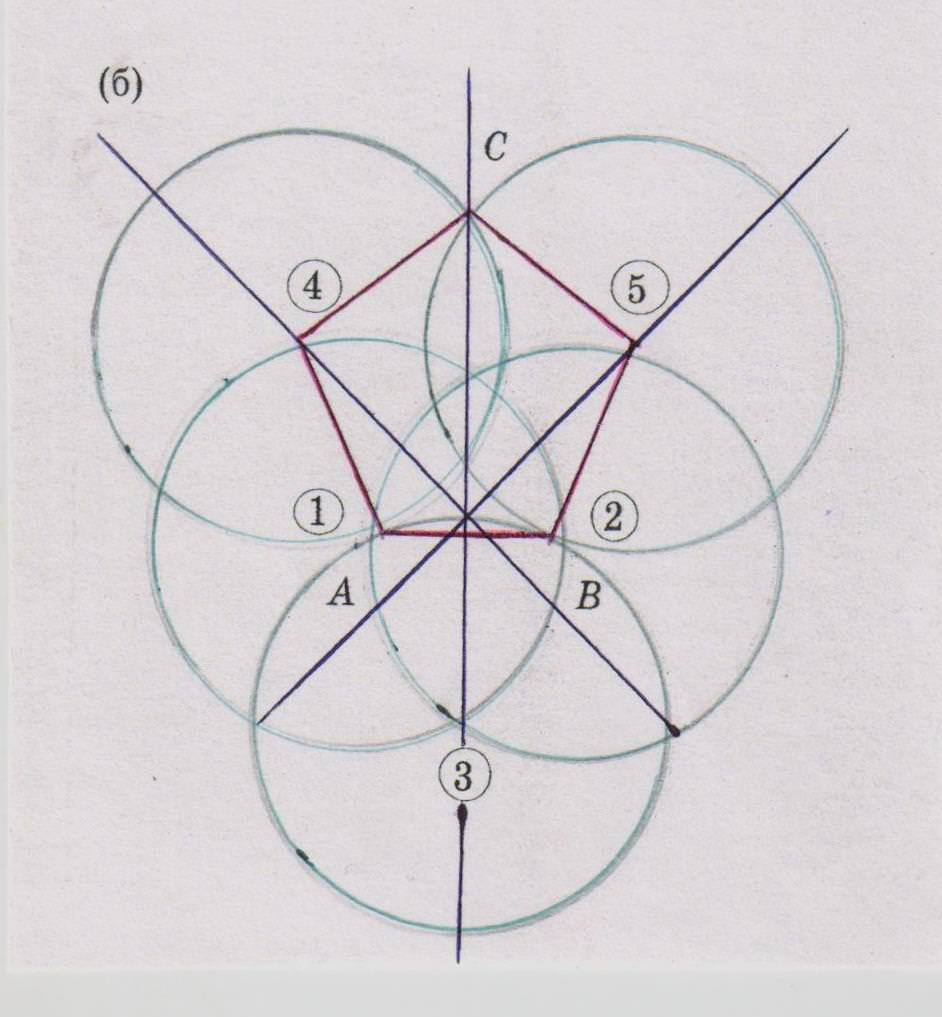
Окружность любого радиуса. Цифрами обозначены последовательные положения ножки циркуля, АВСДК — правильный пятиугольник.

Само построение правильного пятиугольника достаточно сложно, и в тоже время своеобразно.

— Можно ли такое построение назвать красивым?

— А возможно ли, задачу назвать «красивой»?

— Над этим вопросом вы думали дома.

— Я считаю, что красивые задачи существуют, к ним относятся: теорема Виета, пересечение медиан треугольника и, конечно же, теорема Пифагора. Факт, описанный этой теоремой удивителен, прост и неожидан. Красота может доставлять удовольствие не только слуху, взору, но и разуму. Попробуем записать формулу «красивой задачи». Красивая задача = непредсказуемость + простота + неожиданность + …

— А как вы думаете?

Ответы учеников:

1.Мне кажется, что красивая задача это та, которую сложно решить, в то же время просто. Это такая задача, от которой не отойдешь, пока не решишь. А когда решишь, хочется решать еще и еще.

2. Я считаю ту задачу красивой, у которой необычное, запутанное условие и несколько способов решения.

3. В моем понимании, красивая задача при первом знакомстве вызывает страх, а ее решение оказывается удивительно простым… и т.д.

— Вот сейчас мы сможем дописать формулу красивой задачи.

Красивая задача = непредсказуемость + простота + неожиданность + удивление + фантазия + труд + …

— Кто подобрал красивую задачу?

Ученик. Задача. При пересечении диагоналей правильного пятиугольника, в свою очередь образуется правильный пятиугольник. Существуют ли пятиугольники, отличные от правильного, диагонали которого, при пересечении, образуют пятиугольник подобный данному?

Решение (по готовому чертежу).

Эта задача многих ошеломила. Были предложены различные варианты решений, но верных среди них не оказалось.

Необходимо разрядить обстановку, было предложено решение. Искомым пятиугольником является параллельная проекция правильного пятиугольника. Действительно, изображения подобных фигур, лежащих в параллельных плоскостях, подобны. (Это легко доказать, пользуясь определением преобразования подобия и свойствами параллельного проектирования). Решение этой задачи довольно просто. Сначала показалось, что ее решить практически невозможно, но вывод оказался очень простой.

Учитель. Я думаю, что понятие «красивая задача» можно применить и к «золотому сечению». Эта удивительная находка человечества. С древности наблюдая за окружающей природой и создавая произведения искусства, люди искали закономерности, которые позволяли бы определить прекрасное, пытались вывести «формулу красоты».

— Что такое «золотое сечение»?

Определение: Это такое деление отрезка на две неравные части, при котором длина меньшей части, так относится к длине большей части, как длина большей части к длине всего отрезка.

Пример:

В математике ярким примером «золотого сечения» является правильный пятиугольник, или звездчатый пятиугольник он буквально соткан из пропорций, а прежде всего золотой пропорции.

Точка М является «золотым сечением» ВF. В правильном пятиугольнике каждая диагональ делится другой диагональю в отношении «золотого сечения».

Учитель. По мнению многих искусствоведов, художников, скульпторов основные пропорции человеческого тела подчинены законам «золотого сечения».

Ученик. В построении пропорций человека Леонардо да Винчи исходит, прежде всего, из анализа многочисленных измерений самого человека, из его анатомии. Свои исследования Леонардо не успел систематизировать, и они остались рассыпанными в виде рукописных набросков, в которых говорится буквально обо всем на свете, а текст перемежается великолепными рисунками. Вот отрывок текста, которым Леонардо сопровождает рисунок: «Если ты раздвинешь ноги настолько, что убавишься в росте на 1/14, и если ты тогда раздвинешь руки и поднимешь их так, что коснешься средними пальцами макушки головы, то должен ты знать, что центром круга, описанного концами вытянутых членов, будет пупок и что пространство между ногами образует равносторонний треугольник. А пролет распростертых рук человека равен его росту».

Рассказ сопровождается показом по рисунку.

Учитель. А в строении тела человека, можно обнаружить присутствие правильного пятиугольника? И все-таки самым загадочным, самым притягательным произведением искусства Леонардо да Винчи является портрет Моны Лизы.

Ученик. Рассказ по портрету Моны Лизы.

Леонардо да Винчи был великим художником, это признали уже его современники. Портрет Моны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Существует очень много версий об истории этого портрета. Вот одна из них. Однажды Леонардо да Винчи получил заказ от банкира Франческо де ле Джакондо написать портрет молодой женщины, жены банкира, Моны Лизы. Женщина не была красивой, но в ней привлекала простота и естественность облика. Леонардо согласился писать портрет. Его модель была печальной и грустной, но Леонардо рассказал ей сказку, услышав которую, она стала живой и интересной. Кончив сказку, Леонардо взглянул на Мону Лизу, ее лицо озарилось светом, глаза сияли. Потом, точно пробудившись ото сна, она вздохнула, провела по лицу рукой и без слов пошла на свое место, сложила руки и приняла обычную позу. Но дело было сделано, художник пробудил равнодушную статую. Леонардо молча работал, боясь упустить этот момент, этот луч солнца, осветивший его скучную модель…

Кощунственно в портрете, выискать правильные формы, а именно правильные звездчатые пятиугольники, хотя фундаментом послужили именно они, это утверждают искусствоведы. Теория пропорций человека сегодня не умерла, а лишь замерла в ожидании качественно нового скачка, в ожидании перехода от «арифметического» к «компьютерному» выражению.

Иоганн Кеплер говорил, что геометрия владеет двумя сокровищами – теоремой Пифагора и «золотым сечением», если первое из них можно сравнить с мерой золота, то второе с драгоценным камнем.

Учитель. А возможно ли, в музыке, найти этот драгоценный камень — «золотое сечение»?

Ученик. «Золотое сечение» в музыке. Звучит музыка Баха. Хроматическая фантазия и фуга Баха.

Для большей точности результатов мы за единицу меры во времени будем считать не такт, а счетную единицу – в данном случае. Итак, все наши числа в данном примере, написанном в размере 4/4, будут относиться к четвертям. В Хроматической фантазии 79 тактов, то есть 316 четвертых долей. А = 316; А* Н = 195,288;

Золотое сечение приходится, следовательно, на 195-й четверти от начала. Фантазия эта делится на два ясно различимых по характеру отдела: первый из них, который может быть назван прелюдией, после двух энергичных вступительных фраз переходит к целому ряду довольно стремительных рулад и приводит к более спокойному эпизоду – длинному ряду хроматически повышающихся широко арпеджированных аккордов, оканчивающихся на арпеджированном доминантовом трезвучии с задержанием, разрешающимся на второй четверти с ферматой на ней.

Второй отдел состоит из ряда в высшей степени выразительных речитативов, то развивающихся по силе, энергии и размаху до гигантской мощи, то нежных и жалобных, то сердитых и запальчивых, то впадающих в необычную для этой эпохи романтическую мечтательность. Найденный пункт «золотого сечения» с поражающей точностью совпадает с паузой после ферматы на третьей четверти 49-го такта, отделяющей первый отдел от второго (4*48 + 3 = 195). В каждом из двух отделов золотые сечения почти точно совпадают с их кульминационными пунктами.

Проведя небольшое исследование на слух, понимаем, что вся фантазия представляет собою ряд отделов, подчиненных закону золотого сечения. А также мы находим в фантазии Баха еще ряд симметрических подразделений:

Теперь становится понятно, почему эта кажущаяся столь свободной импровизационная форма при всей свободе и растяжимости своих темпов, при всем разнообразии входящих в нее мелодических рисунков и фигурационных мотивов и при всей пестроте своего модуляционного плана производит впечатление глубочайшего, чисто психического единства. Она, оказывается, сотворена по естественным законам природного формообразования, подобно человеческому организму, в котором совершенно так же господствуют оба закона – закон золотого сечения и закон симметрии, с такими же мелкими художественными неточностями в индивидуальном строении живого тела, которыми оно отличается от мертвых форм отвлеченного или фабричного происхождения.

Итог урока: Красота не является избранницей только музыки и искусства. Красота есть повсюду. Есть она и в науке, и в особенности в ее жемчужине – математике. А значит, «царица всех наук» откроет перед нами сказочные сокровища красоты.

Домашнее задание: Подготовить небольшое сообщение:

1вариант «Золотое сечение» в скульптуре.

2 вариант «Золотое сечение» в архитектуре.

Список использованной литературы:

1. Барышников Н.В. «Параметры обучения межкультурной коммуникации в средней школе», ИЯШ №2, 2002

2. Башмаков М.И. «Алгебра и начала анализа». – М.: Просвещение, 1993

3. Волошинов А.В. «Математика и искусство». – М: Просвещение, 1992

4. Еженедельная учебно – методическая газета «Математика»: 40/97, 41/97, 17/99, 33/99, 2/о1, 19/01, 31/01.

5. Кобалевский Д.Б. Программа по музыке. 4-8 кл.. – М: Музыка, 1983

6. Математика в школе – 6/89, 3/94, 4/10.

7. Программы для общеобразовательных школ, гимназий, лицеев. Математика. 5-11классы. – М: Дрофа, 2004

8. Розинов Э. Статьи о музыке

9. Философский словарь (под редакцией И.Т.Фролова). – М.: Политическая литература

10. Чурилов И.И. Гуманитарный потенциал математики. — Пермь,1998

11. Шюре Э. Великие посвященные (перевод с французского Е.Писаревой) Рейтинг издания 1914г.

Иллюстрации:

1. Золотое сечение в картине Леонардо да Винчи «Джоконда». Сайт «Энциклопедия замечательных людей и идей», раздел «Золотое сечение». http://www.adc—people.com/data/leonardov/

2. Леонардо да Винчи. Витрувианский человек, 1490 г., Галерея Академии, Венеция. http://ru.wikipedia.org/ статья Витрувианский человек

3. Леонардо да Винчи. Портрет госпожи Лизы Джокондо, Лувр, Париж. http://ru.wikipedia.org/ статья Мона Лиза.