Тамбовское областное государственное автономное образовательное учреждение – общеобразовательная школа – интернат
«Мичуринский лицей»
Уроки-практикумы по тригонометрии .
(материалы для учащихся 10 класса)
подготовила
учитель математики
Кузнецова Оксана Евгеньевна
Г. Мичуринск
2012год.
Пояснительная записка.
Предлагаемые материалы к урокам-практикумам по тригонометрии позволят учителю организовать на уроках тренинг-практикумы двух типов. Для практикумов,проводимых в начале изучения темы даются системы циклов взаимосвязанных задач.Их цель- не только отработка учащимися образовательного стандарта или материала максимально к нему близкого, но и формирование умений и навыков делать выводы , усматривать закономерности,»двигаясь» по материалу в направлении от простого к сложному. При этом ученик видит,на что следует обратить внимание. что следует доработать. Как оценивать такую работу, каждый учитель решает самостоятельно. Второй тип практикумов – практикумы
по накопительной системе. Их целесообразно проводить за несколько уроков до контроля. Порядок их проведения заключается в следующем: перед учеником три варианта работы разной степени сложности, он может выбирать любое задание из любого варианта, зная ,что за каждое задание он получает определенное количество баллов.Т.е. учащийся выстраивает индивидуальный маршрут работы. На таких уроках максимально отлажена обратная связь т.к. учитель проверяет правильность выполнения каждого задания, анализирует допущенные ошибки и т.д.
Если класс многочисленный, то можно разбить его на группы, каждая из которых
реализует свой маршрут. Критерий оценивания таких работ приводится.
https://rezjrc73.pedgazeta.ru/mydocs.php
Практикум 1
(40 мин.)
Вариант А
![]()
1 Переведите угол в 2 рад. В градусную меру.
2 Определите знак выражения sin![]() π cos
π cos![]() π tg
π tg ![]() π ctg
π ctg![]() π.
π.
3 Найдите cosα,tgα,ctgα, если sinα =![]() , если
, если ![]() π<α<π.
π<α<π.
4 Упростите а) 1-sin2x+ctg2xsin2x
б) (1+ctg2x) -1+(1+tg2x)-1
5 Вычислите sin2(π/4)+tg(-π/3)-cos(π/3)+ctg(π/6).
6 Какие значения может принимать выражение![]() ?
?
Вариант В
1 Вычислите ![]() cos
cos![]() π-sin
π-sin![]() π-3tg(-9π).
π-3tg(-9π).
2 Найдите значение выражения sin3α+cos3α ,если sinα+cosα=1/2.
3 Докажите тождество: sin2αcos2β – cos2αsin2β = sin2α – sin2β.
4 Найдите значение выражения![]() , если tg=2,x- угол первой четверти.
, если tg=2,x- угол первой четверти.
5 Сколько углов α на промежутке [-20π;30π] , удовлетворяющих условию sinα=0?
6 Задайте формулой α гдеР α –точка тригонометрической окружности, симметричная точке Рπ/6.
Вариант С
1 Упростите выражение![]() + sin2x + 1, если
+ sin2x + 1, если ![]() <x<
<x<![]() .
.
2 Вычислите ![]() , если tg
, если tg![]() =3.
=3.
3 Вычислите tg4![]() + ctg4
+ ctg4![]() , если tg
, если tg![]() —ctg
—ctg![]() =m.
=m.
4 Найдите наименьшее значение выражения1-cos![]() -2sin2
-2sin2![]() .
.
5 Найдите множество дoпустимых значений переменой в выражении![]() .
.
Практикум 2 ( 60 мин.)
1 Вариант 2 Вариант 3 Вариант
ЦИКЛ 1 ЦИКЛ 1 ЦИКЛ 1
Упростите Упростите Упростите
1) sin(![]() —
—![]() ) 1)cos(
) 1)cos(![]() -2x) 1) tg(
-2x) 1) tg(![]() —
—![]() )
)
2) sin(![]() —
—![]() ) 2)cos(2x-
) 2)cos(2x-![]() ) 2) tg (
) 2) tg (![]() —
—![]() )
)
3) 3sin2(![]() —
—![]() ) 3) cos2(2x-270◦) 3) tg4(
) 3) cos2(2x-270◦) 3) tg4( ![]() —
—![]() )
)
4) sin5 (![]() —
—![]() ) 4) cos3(270◦-2x) 4)tg3(
) 4) cos3(270◦-2x) 4)tg3(![]() —
—![]() )
)
ЦИКЛ 2 ЦИКЛ 2 ЦИКЛ 2
Вычислите Вычислите Приведите cos0,7![]() к 5) cos 60 ◦ 5) sin
к 5) cos 60 ◦ 5) sin![]() тригонометрической
тригонометрической
функции угла
6)cos(180◦– 60◦) 6)sin(![]() +
+![]() )
)
7) cos120 ◦ 7)cos![]() 5) из промежутка (0;
5) из промежутка (0;![]() )
)
8)cos(-480◦) 8) cos(-![]() ) 6) из (
) 6) из (![]() ;2
;2![]() )
)
7) из (![]()
![]() ;3
;3![]() )
)
8) из (-![]() ;0)
;0)
ЦИКЛ 3 ЦИКЛ 3 ЦИКЛ 3
9) Упростите: 9) Упростите: 9) Упростите:
cos2x+cos(3![]() -2x)
-2x)![]()
![]() tg
tg![]() tg(
tg(![]() —
—![]() ) sin2
) sin2![]() +sin2(
+sin2(![]() +
+![]() )
)
Вычислите : Вычислите Вычислите
10)cos20◦+cos160◦+ 10)tg10◦tg80◦ 10) cos215◦+cos275◦
+cos180◦
11)cos20◦+cos40◦+cos60◦+…+ 11)tg19◦tg20◦tg30◦…tg80◦ 11)sin210◦+sin215◦+sin220◦+…+
+cos160◦+cos180◦ +sin285◦+sin290◦
4 ЦИКЛ 4 ЦИКЛ 4 ЦИКЛ 4
Упростите Упростите Упростите
12)sin4![]() +cos4(
+cos4(![]() —
—![]() ) -1 12)
) -1 12)![]() 12)cos6(
12)cos6(![]() -x)+sin6(
-x)+sin6(![]() +x)-1
+x)-1
13) 13)
13)  13
13![]()

ПРАКТИКУМ № 3 ( 80 мин)
Вариант А
1 Вычислите sin15◦ ( 2 способа).
2 Вычислите![]() .
.
3 Дано: sin![]() =-
=-![]() ,
, ![]() <
<![]() <
<![]() . Вычислите sin(
. Вычислите sin(![]() —
—![]() ).
).
4 Вычислите а)![]() б)
б) .
.
5 Вычислите sin![]() cos
cos![]() .
.
6 Упростите 2sin2![]() + cos
+ cos![]() ( два способа).
( два способа).
7 Докажите тождество ctg![]() —sin2
—sin2![]() =ctg
=ctg![]() cos2
cos2![]() .
.
8 Найдите наибольшее значение выражения sin![]() .
.
Вариант В
1 Упростите ![]() .
.
2 Найдите значение выражения cos40◦+tg20◦sin40◦.
3 Упростите ![]() .
.
4 Вычислите cos![]() .
.
5 Упростите ![]() , 0
, 0![]() .
.
6 Возможно ли равенство 3sin x+4cosx=7 ?
Вариант С![]()
1 Дано: sin(![]() +
+![]() )=
)=![]() ,
,![]() <
<![]() <
<![]() . Найти sin
. Найти sin![]() .
.
2 Найдите значение выражения sin4![]() +cos4
+cos4![]() +sin4
+sin4![]() +cos4
+cos4![]() .
.
3 Упростите 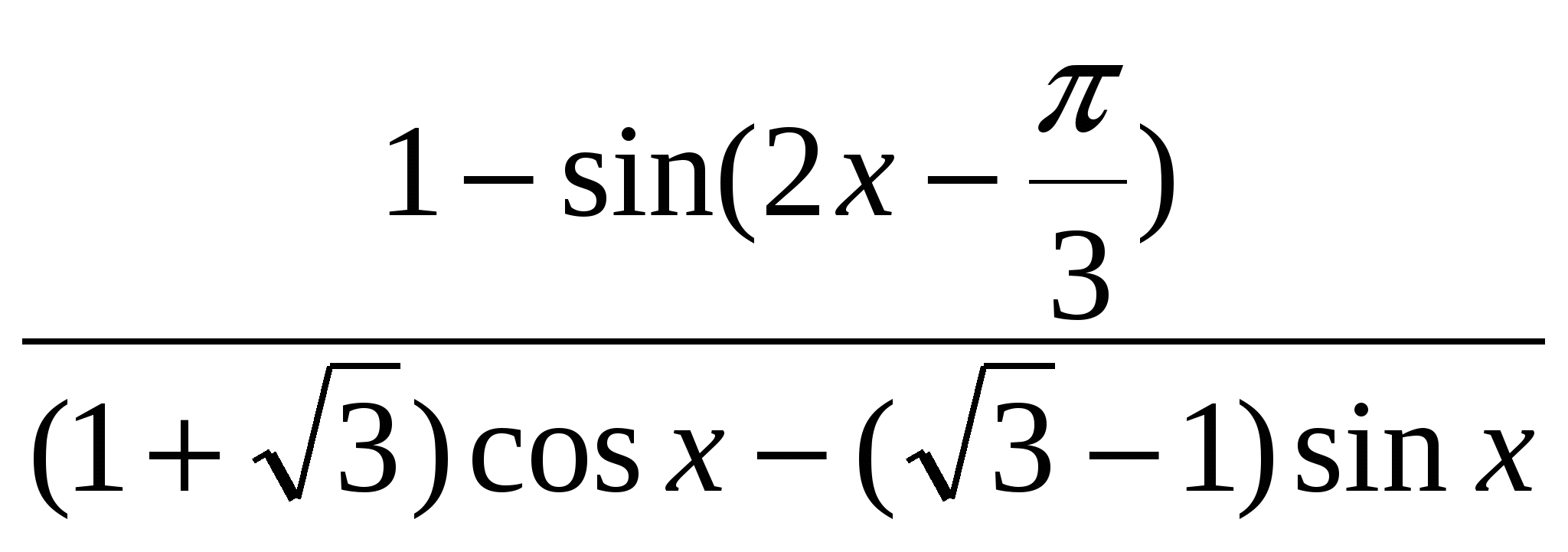 .
.
4 Докажите тождество cos![]() cos
cos![]() cos
cos![]() …cos
…cos ![]() =
= ![]() .
.
5 Упростите : tg9◦+tg15◦-tg27◦—ctg27◦+ctg9◦+ctg15◦ .
Практикум №4
Преобразование суммы тригонометрических выражений в произведение.
Преобразование произведения тригонометрических выражений в сумму. (40мин.)
Вариант 1 Вариант 2 Вариант 3
ЦИКЛ 1 ЦИКЛ 1 ЦИКЛ 1
Представьте в виде произведения:
1) cos![]() 1) sin
1) sin![]() 1) sin
1) sin![]()
2) sin![]() 2) cos
2) cos![]() 2) cos
2) cos![]()
3) ![]() 3) cos
3) cos![]() 3)
3) ![]()
4) ![]() 4) 2cos
4) 2cos![]() 4)
4) ![]()
5) ![]() 5)
5) ![]() 5) 3 —
5) 3 —![]()
6)  6)
6)  6)
6) ![]()
ЦИКЛ 2 ЦИКЛ 2 ЦИКЛ 2
Представьте в виде суммы:
7) ![]() 7)
7) ![]() 7)
7) ![]()
8) ![]() 8)
8) ![]() 8)
8) ![]()
9) sin![]() 9)
9) ![]() 9)
9) ![]()
Докажите тождество
10)![]() ( 1 вариант)
( 1 вариант)
10)![]() ( 2 вариант)
( 2 вариант)
10)![]() ( 3 Вариант)
( 3 Вариант)
Практикум №5
Преобразование тригонометрических выражений и доказательство тождеств.
(80мин.)
Вариант А
Упростите:![]() .
.
Найдите значение выражения: 2(![]() , если sin
, если sin![]() .
.
3) Упростите выражение ![]() .
.
4) Найдите: tgx, если sinx=![]() ,0<x<
,0<x<![]() .
.
5)Докажите тождество: 1-![]() .
.
6) Докажите тождество:![]()
7) Упростите:
Вычислите: cos422,5◦-sin422,5 ◦ .
Вычислите: 1-2![]() .
.
Вариант В
1) Упростите: 0,125-![]()
2) Вычислите: ![]() .
.
3) Вычислите: 
4)Упростите (1-2sin![]()
5) Найдите значение выражения:![]()
6) Докажите тождество:![]()
7) Упростите выражение:![]()
8) Докажите неравенство: sin(x+2)cos(x-2)<sin(x+3)cos(x-3)
Вариант С
1) Упростите выражение sin![]() .
.
2) Найдите sin18![]() .
.
3) Вычислите значение выражения sin![]()
4) Найдите ![]() , если sin
, если sin![]() -4 четверти.
-4 четверти.
5) Решить неравенство:![]()
Практикум №6
Графики и свойства тригонометрических функций (80 мин.)
Вариант 1 Вариант 2 Вариант 3
ЦИКЛ 1
Для данной функции
| y = sin | y = |
Ответьте на вопросы:
1) область определения функции,
2) множество значений функции,
3) исследовать функцию на четность,
4) период функции,
5) множество значений функции на промежуте: а) ![]() , б)
, б) ![]() ,
,
6) промежутки монотонности.
ЦИКЛ 2
Постройте графики функций.
| 1) y = sin x | 1) y = tg x | |
| 2) y = 2cos x – 1 | 2) y = — | 2) y = tg x – 2 |
| 3) y = cos 2x | 3) y = sin | 3) y = tg |
| 4) y = 2cos(x + | 4) y = -sin( x + | 4) y = tg ( x — |
| 5) y = — | 5) y = | 5) y = -2tg(2x — |
| 6) y = — | 6) y = | 6) y = -2tg(2x — |
ЦИКЛ 3
Определите период функции.
| 1) y = ctg | 1) y = cos | |
| 2) y = tg 2x + cos 3x | 2) y = cos 2x-sin 6x | 2) y = cos |
| 3) y = sin 2x cos 3x | 3) y = cos2x sin 6x | 3) y = cos |
| 4) y = | 4) y = | 4) y = |
| 5) y = tg 2x cos 3x | 5) y = ctg | 5) y = ctg |
Практикум № 7
Простейшие тригонометрические уравнения.(60-80мин.)
Цикл 1
Решите уравнения.
Вариант 1 Вариант 2 Вариант 3
| 1) cos(x-1) = -1 | 1) cos( | |
| 2) sin 2x = -1/2 | 2) cos(x-1)= -1/2 | 2) cos( |
| 3) sin2x = 0 | 3) cos(x-1) = 0 | 3) cos( |
| 4) sin 2x = 1./2 | 4) cos(x-1) = 1/2 | 4) cos( |
| 5) sin2x = 1 | 5) cos(x-1) = 1 | 5) cos( |
| 6) sin2x = a | 6) cos(x-1) = a | 6) cos( |
| 7) | 7) | 7) |
Цикл 2
Решите уравнения.
| 1) ctg( | 1) tg7x = -1 | |
| 2) tg(3-x) = ½ | 2) ctg( | 2) tg7x = -1/2 |
| 3) tg(3-x) = 0 | 3) ctg( | 3) tg7x = 0
|
| 4) tg(3-x) = -1/2 | 4) ctg( | 4) tg7x = 1/2 |
| 5) tg (3-x) = -1 | 5) ctg( | 5) tg7x = 1 |
| 6) Найдите область определения уравнения
| 6) Найдите область определения уравнения
| 6) Найдите область определения уравнения
|
| 7) Сравните области определения уравнений
ctg(3-x)=1/2. |
tg( |
|
Цикл 3
Для данного уравнения
| сos | cos2xcos( |
ответьте на вопросы:
наименьший положительный корень уравнения,
наибольший отрицательный корень уравнения,
3) количество корней уравнения на промежутке(0;![]() ),
),
4) корень, ближайший к 1,
5) корни, удовлетворяющие неравенству x2<4.
Цикл 4
Решите уравнение.
| 1) cos2x-3/4 = 0 | 1)sin2x-3/4 = 0 | |
| 2) cos x — | 2) sin x – 1.2 = 0 | 2) cos x -1/2 = 0 |
| 3) | 3) | 3) |
Практикум № 8
Решение простейших тригонометрических уравнений.( 40 мин.)
Вариант А
Решите уравнение:
sin(![]()
2cos![]()
2sin(![]()
ctg(![]()
5) Укажите все корни уравнения sin x cos(3![]() —x)=
—x)= ![]() из промежутка (0;2
из промежутка (0;2![]() ) .
) .
Вариант В
Укажите все неположительные корни уравнения  .
.
Решите уравнение : (![]() .
.
Решите уравнение : sin((x+![]() .
.
4) Решите уравнение: cos![]()
![]()
5) Решите уравнение с параметром sin(x-5) = m.
Вариант С
Решите уравнение: cos 2x tgx + tg x— cos 2x = 1.
2) Решите уравнение с параметром sin(x2+2x) = 2m.
.3) Решите уравнение с параметром ctg![]() .
.
4) Решите уравнение:![]()
Практикум №9
Взять залания на усмотрение учителя из практикума № 6,заменив знак «=» на знаки неравенств.
Практикум № 10.
Решение тригонометрических уравнений. ( 40 мин,)
Вариант А.
Решите уравнения:
3sin22x+10sin2x+3 = 0,
cos2x+3sinx = 2,
sin(![]() .
.
Найдите сумму корней уравнения sin ![]() =
=![]() , принадлежащих промежутку
, принадлежащих промежутку ![]() .
.
Решите уравнение: sin2x—sin2x=3cos2x.
Решите уравнение 6sin2x+5sinxcosx+3cos2x=2 и укажите количество его корней из интервала ![]() .
.
Вариант В.
Решите уравнения:
1) ![]()
2) ![]()
3) ![]()
4) 4sin4x+3=7tg2x(1-sin2x),
5) ![]() .
.
Вариант С.
Найдите все корни уравнения (cos![]()
Укажите наименьшее значение параметра b, при котором уравнение cos2x-(3+2b)cosx+6b=0 имеет хотя бы один корень.
Решите уравнение:![]() .
.
Практикум №11.
Решение тригонометрических уравнений.
Вариант А.
1) Укажите корень уравнения cos![]() , принадлежащий промежутку
, принадлежащий промежутку ![]() .
.
2) Укажите наименьший положительный корень уравнения 3cosx+sin(-2x)=0.
3) Решите уравнение: tg3x=tgx.
4) Решите уравнение:sin2x+2sinx=cosx+1.
5) Решите уравнение: ![]() .
.
Вариант В.
Решите уравнение:
cos2![]() +0,5
+0,5![]() ,
,
sin3x+cos3x=3sinxcosx-1,
sin2x+0,25sin22x-sinxsin22x=0,
tg![]()
Найдите сумму корней уравнения sin2![]() из отрезка
из отрезка ![]() .
.
Вариант С.
Решите уравнение: cos![]()
![]()
2) Укажите все решения уравнения 4sin2x(1+cos2x)=1-cos2x, удовлетворяющие неравенству x2<4.
3) При каких значениях параметра a уравнение cos2x— acosx=0 имеет хотя бы одно решение?
Практикум №12.
Решение тригонометрических уравнений. (40мин.)
Вариант А.
Решите уравнения:
2cos![]()
![]()
3) 5cos2x+6sinx-6=0,
4) 3sin2x—sinxcosx=2,
5)![]() .
.
Вариант В.
Решите уравнения:
sin![]() =
=![]() ,
,
5sin![]() ,
,
3) ![]()
4) 13sin2x+84sin2x-13cos2x+1=![]() ,
,
5) 3tg![]() .
.
Вариант С.
Решите уравнение: cos x+cos</span
