Подготовила: учитель математики
Категория: высшая
Тихончук Людмила Юрьевна
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №3»
Станица Старощербиновская Щербиновского района Краснодарского края
Подготовка к ЕГЭ задание В10
Тема: «Теория вероятностей»
для 10-11 класса
2013 г.
Теория вероятностей – один из наиболее важных прикладных разделов математики. Многие явления окружающего нас мира поддаются описанию только с помощью теории вероятностей. В России она была возвращена в школу стандартом в 2004 году и пока остается новым разделом. Учащиеся и даже учителя пока еще испытывают определенные трудности при изучении теории вероятностей и статистики, связанные с отсутствием глубоких традиций преподавания и малочисленностью учебных материалов. Второй год эта тема стала присутствовать на экзамене. В разработке представлены задания рассчитанные на любой уровень знаний и поможет не только при подготовке к экзамену, но и как дидактический материал при изучении курса теории вероятностей в основной и полной средней школе.
Содержание.
Раздел №1 ( для учителя )
Задания с решениями.
Раздел №2 ( для учащихся )
Проверка уровня усвоения материала в двух вариантах.
Ключи к разделу №2
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 0,75 | 0,25 | 0,33 | 0,15 | 0,3 | 0,4 | 0,2 | 0,32 | 0,4 | 0,6 |
| 2 | 0,25 | 0,11 | 0,33 | 0,125 | 0,1 | 0,6 | 0,8 | 0,35 | 0,6 | 0,7 |
Раздел №1
Классическое определение.
Вероятность события (Р(А)) – это численная мера объективной возможности его появления.
Вероятностью Р наступления случайного события А называется отношение m/n, где n – число всех возможных исходов эксперимента,
а m – число всех благоприятных исходов:
Р(А)= m/n.
Следует заметить, что всегда выполняется двойное неравенство  , поэтому вероятность любого события А лежит на отрезке
, поэтому вероятность любого события А лежит на отрезке  , то есть
, то есть 
Не стоит забывать, что сумма противоположных событий всегда равна 1,
то есть 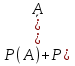 .
.
Задачи для учителя
1.В магазине оптики при покупке фотоаппарата в качестве подарка к нему дарится чехол, который случайным образом выбирается из ящика. В ящике находятся чехлы разного цвета: 12 — черных, 15 – бежевых, 17 красных и 16 – в клеточку. Найдите вероятность того, что покупатель вынет из этого ящика черный чехол.



2. На школьном концерте от 1 «А» выступают семь гномов и Белоснежка – поют песню; от 1 «Б» выступают три медведя – танцуют; от 1 «В» выступает Буратино со стихом. Дед Мороз попросил каждого выступающего бросить в его варежку букву своего класса. Первая вытянутая буква определит, какой класс будет открывать концерт. Найдите вероятность того, что первым номером программы будет песня. (Ответ округлите до сотых).



3. Елочная гирлянда состоит из 10 желтых, 15 зеленых, 20 красных и 5 синих лампочек. Каждая лампочка перегорает с одинаковой частотой. Для их смены необходимо закупить запасные. Найдите вероятность того, что в какой-то момент времени перегорит красная лампочка.



4. В барабане лотереи шары с номерами от 1 до 16. Какова вероятность того, что номер случайно выбранного шара будит делиться на 4?



5. Крупье вытаскивает наугад из 36-ти карточной колоды 6 карт и кладет их на стол. Среди вытащенных карт 3 пиковой масти и 3 бубновой масти. Какова вероятность, что седьмая вытащенная им карта будет бубновой масти? (Колода игральных карт содержит по 9 карт каждой из четырех мастей).


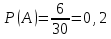
6. В урне находится 5 шаров: 2 белых и 3 черных. Наугад вытаскивают 2 шара. Какова вероятность того, что вытащенные шары будут черного цвета?
Пояснение
Часто ученики допускают в таком типе задач ошибку 
Необходимо объяснить, что шары хоть и одного цвета, но каждый из них индивидуален.
Б1 Б2 Ч1 Ч2 Ч3
Найдем сначала n – число всех возможных исходов эксперимента
Б1 Б2
Б1Ч1
Б1Ч2
Б1Ч3
Б2Ч1
Б2Ч2
Б2Ч3
Ч1 Ч2
Ч1Ч3
Ч2 Ч3

 (Ч1 Ч2 и Ч1Ч3 и Ч2 Ч3 )
(Ч1 Ч2 и Ч1Ч3 и Ч2 Ч3 )

7. Перед началом первого тура соревнований по международным шашкам участников соревнований разбивают на игровые пары случайным образом (по жребию). Всего в соревнованиях участвует 26 спортсменов, среди которых 9 участников из Польши, в том числе Павел Калиновский. Найдите вероятность того, что в первом туре Калиновский будет играть с шашистом из Польши.


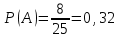
8. В корзине лежат 80 яблок трех разных сортов: 56 красных, и поровну желтых и
зеленых. С какой вероятностью случайно вынутое из корзины яблоко окажется
зеленым?



9. В кармане у Пети было 3 монеты по 1 рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то 2 монеты в другой карман. Найдите вероятность того, что все монеты по 1 рублю лежат в кармане.
Задача схожа по решению с №6. Можно использовать обозначения:
11 12 13 21 22
взяли осталось
11 12 13 21 22
11 13 12 21 22
11 21 12 13 21
11 22 12 13 21
12 13 11 21 22
12 21 1113 22
12 22 1113 21
13 21 11 12 22
13 22 11 12 21
21 22 11 12 13



10. Почти одновременно 8 человек, в том числе Андрей, заказали по телефону пиццу, все разных видов. Оператор перепутал 3 и 5 заказы. С какой вероятностью Андрею привезут его пиццу?



Радел №2
Вариант №1
1. В магазине оптики при покупке фотоаппарата в качестве подарка к нему дарится чехол, который случайным образом выбирается из ящика. В ящике находятся чехлы разного цвета: 5 — черных, 7 – бежевых, 8 красных. Найдите вероятность того, что покупательница вынет из этого ящика чехол не черного цвета.
2. На школьном концерте от 1 «А» выступают семь гномов и Белоснежка – поют песню; от 1 «Б» выступают три медведя – танцуют; от 1 «В» выступает Буратино со стихом. Дед Мороз попросил каждого выступающего бросить в его варежку букву своего класса. Первая вытянутая буква определит, какой класс будет открывать концерт. Найдите вероятность того, что первыми будут выступать медведи. (Ответ округлите до сотых).
3. Елочная гирлянда состоит из 60-ти лампочек разного цвета: 25 желтых, 10 зеленых, 5 красных, остальные — синие. Каждая лампочка перегорает с одинаковой частотой. Для их смены необходимо закупить запасные. Найдите вероятность того, что в какой-то момент времени перегорит синяя лампочка. (Ответ округлите до сотых).
4. В барабане лотереи шары с номерами от 1 до 20. Какова вероятность того, что номер первого вытащенного шара будит делиться на 6?
5. Крупье вытаскивает наугад из 36-ти карточной колоды 6 карт пиковой масти подряд и кладет их на стол. Какова вероятность, что седьмая вытащенная им карта будет бубновой масти? (Колода игральных карт содержит по 9 карт каждой из четырех мастей).
6. В урне находится 5 шаров: 2 белых и 3 черных. Наугад вытаскивают 2 шара. Какова вероятность того, что вытащенные шары будут одного цвета?
7. Перед началом первого тура соревнований по бадминтону участников соревнований разбивают на игровые пары случайным образом (по жребию). Всего в соревнованиях участвует 36 спортсменов, среди которых 8 участников из Украины, в том числе Николай Колоденко. Найдите вероятность того, что в первом туре Николай Колоденко будет играть со своим соотечественником.
8. Научная конференция проводится в течение 3 дней и включает 75 докладов. В первый день запланировано 27 докладов, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жребием. Какова вероятность, что доклад профессора П состоится в третий день конференции?
9. В кармане у Пети было 3 монеты по 1 рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то 2 монеты в другой карман. Найдите вероятность того, что обе двухрублевые монеты лежат в одном кармане.
10. Почти одновременно 5 человек, в том числе Петя, заказали по телефону пиццу, все разных видов. Оператор перепутал 3 и 4 заказы. С какой вероятностью Пете привезут его пиццу?
Вариант №2
1.Меховой дом выставил на продажу 7 шуб 42-го размера, 15 шуб 44-го размера и 6 шуб 46-го размера. Из этого набора случайным образом отобрали шубу и повесили ее на витрину. Найти вероятность того, что на витрине окажется шуба 42- го размера.
2. На школьном утреннике Дед Мороз в игре догонялки с закрытыми глазами ловит учащихся переодетых в костюмы. Из них: 6 зайчиков, 4 пирата, 3 медведя, 7 снежинок,
5 русалочек, белочка и лисичка. Определите, с какой вероятностью первый пойманный
учащийся будет в костюме медведя. (Ответ округлите до сотых).
3. В коробке с елочными украшениями находятся 90 одинаковых шаров, отличающихся только цветом, из них: 15 шаров синих, 15 — красных, 30 — серебряных, остальные – золотые. Найдите вероятность того, что наудачу вынутый из коробки шар будет золотым. (Ответ округлите до сотых).
4. Два человека независимо друг от друга загадывают по одному натуральному числу от 1 до 8. Какова вероятность того, что сумма загаданных ими чисел равна 9?
5.Крупье вытаскивает наугад из 36-ти карточной колоды 6 карт пиковой масти подряд и кладет их на стол. Какова вероятность, что седьмая вытащенная им карта также будет пиковой масти? (Колода игральных карт содержит по 9 карт каждой из четырех мастей).
6. В урне находится 5 шаров: 2 белых и 3 черных. Наугад вытаскивают 2 шара. Какова вероятность того, что вытащенные шары будут разного цвета?
7. Перед началом первого тура соревнований по фехтованию участников соревнований разбивают на пары случайным образом (по жребию). Всего в соревнованиях участвует 46 спортсменов, среди которых 10 участников из Франции, в том числе Жюльен Дюпон. Найдите вероятность того, что в первом туре Жюльен будет соревноваться не со своим соотечественником.
8. Научная конференция проводится в течение 3 дней и включает доклады участников. В первый день запланировано 27 докладов, во второй – 21, в третий – 12 докладов. Порядок докладов определяется жребием. Какова вероятность, что доклад профессора П состоится во второй день конференции?
9. В кармане у Пети было 3 монеты по 1 рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то 2 монеты в другой карман. Найдите вероятность того, что обе двухрублевые монеты лежат в разных карманах.
10. Почти одновременно 10 человек, в том числе Ваня, заказали по телефону пиццу, все разных видов. Оператор перепутал 3,4 и 10 заказы. С какой вероятностью Ване привезут его пиццу?
Список использованной литературы
1.ЕГЭ 2012 Математика .Задача В10.Теория вероятностей. Рабочая тетрадь/
Под редакцией А.Л.Семенова и И.В.Ященко.- М.: МЦНМО, 2012.
2. Тексты КДР 2010-2013 г . Автор составитель: Краснодарский краевой институт дополнительного профессионального педагогического образования.
