Негосударственное общеобразовательное учреждение
«Миасская средняя школа – интернат № 14 ОАО «РЖД»»
Челябинской области
Конспект урока по геометрии
в 7 классе
«Медианы, биссектрисы и высоты треугольника»
подготовила
учитель математики
Зенбицкая Елена Евгеньевна
г. Миасс
2013
Открытый урок геометрии в 7 классе.
Тема. Медианы, биссектрисы и высоты треугольника.
Цель: Добиться чёткого понимания, что такое медианы, биссектрисы и высоты
треугольника. Опытным путём установить, что точки пересечения медиан,
биссектрис и высот в правильном треугольнике совпадают,
в равнобедренном треугольнике лежат на одной прямой,
в разностороннем треугольнике являются вершинами нового треугольника.
Оборудование: модели треугольников, изготовленные учащимися дома, презентация.
План урока.
1. Организационный момент. Запись домашнего задания. (построить медианы и высоты в оставшихся треугольниках)
2. Устная работа. (10 минут)
а) Готовые чертежи на доске.
| Д M K
O
P N |
Решения устных задач.
1 . В треугольниках АСВ и ADB: АС = AD по условию, ∆АВС = ∆ABD по двум
. В треугольниках АСВ и ADB: АС = AD по условию, ∆АВС = ∆ABD по двум
АВ – общая сторона, => сторонам и углу между
<САВ = < BAD по условию. ними.
2 . В треугольниках МОК и NOP: MO = ON по условию, ∆MOK = ∆NOP по двум
. В треугольниках МОК и NOP: MO = ON по условию, ∆MOK = ∆NOP по двум
OK = OP по условию, => сторонам и углу между
<MOK = < NOP — вертикальные. ними.
б) Фронтальная работа.
1. Определения, каких понятий учили к этому уроку?
(медианы, биссектрисы, высоты)
2. Дать определение медианы.
3. Дать определение биссектрисы.
4. Дать определение высоты.
5. Вы дома выполняли практическую работу: строили медианы биссектрисы и высоты
треугольников. В каких треугольниках вы их строили?
(В прямоугольных разносторонних и равнобедренных, остроугольных равносторонних, равнобедренных и разносторонних, тупоугольных равнобедренных и разносторонних).
На что обратили внимание?
(Медианы, биссектрисы и высоты пересекаются в одной точке).
Как сформулировать это свойство? (Показать слайды)
3. Практическая работа. (25 минут)
Дома вы строили в каждом треугольнике по три отрезка либо медианы, либо биссектрисы, либо высоты. Сейчас вы будете строить в одном треугольнике и медианы, и биссектрисы, и высоты. Построить в семи видах треугольников по девять отрезков вы не успеете, поэтому будете строить каждый только в одном треугольнике, а остальные построите дома. Чтобы охватить все виды треугольников, я скажу, кто с каким треугольником будет работать:
а) равносторонний — Арутюнян, Пянковский

б) равнобедренный остроугольный — Амирова (на доске)

в) равнобедренный прямоугольный – Зеленин



г) равнобедренный тупоугольный — Королюк, Доможирова

д) разносторонний остроугольный – Васютина









е) разносторонний прямоугольный — Шестакова, Иванов
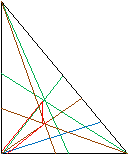
ж) разносторонний тупоугольный – Савельев
Построили. Теперь каждый расскажет, что у него получилось, и какой вывод он сделал.
Выводы: точки пересечения медиан, биссектрис и высот
в правильном треугольнике совпадают,
в равнобедренном треугольнике лежат на одной прямой,
в разностороннем треугольнике являются вершинами нового треугольника.
Выставить оценки.
4. Самостоятельная работа.
Работа по карточкам четырёх вариантов: по готовым чертежам в разных видах треугольников
определить, какой отрезок является медианой, какой — биссектрисой, а какой — высотой.
Тетради сдать на проверку.

РАВНОСТОРОННИЙ
РАВНОБЕДРЕННЫЕ



ОСТРОУГОЛЬНЫЙ ПРЯМОУГОЛЬНЫЙ ТУПОУГОЛЬНЫЙ
РАЗНОСТОРОННИЕ




ОСТРОУГОЛЬНЫЙ ПРЯМОУГОЛЬНЫЙ ТУПОУГОЛЬНЫЙ



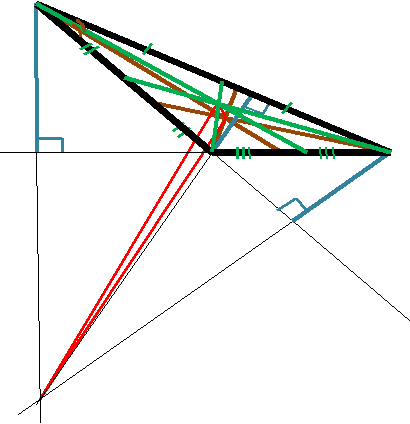
Т упоугольный равнобедренный
упоугольный равнобедренный
Тупоугольный разносторонний

В равнобедренном треугольнике точки пересечения медиан, биссектрис и высот лежат на одной прямой — высоте, биссектрисе и медиане, проведённой к основанию треугольника.

В равностороннем треугольнике медианы, биссектрисы и высоты совпадают и пересекаются водной точке.
равностороннем треугольнике медианы, биссектрисы и высоты совпадают и пересекаются водной точке.
Р авнобедренный Равносторонний
авнобедренный Равносторонний
 остроугольный
остроугольный






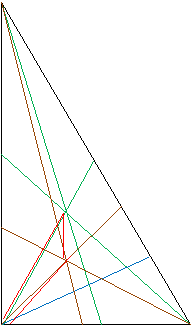
Равнобедренный Разносторонний
прямоугольный прямоугольный


Разносторонний остроугольный

В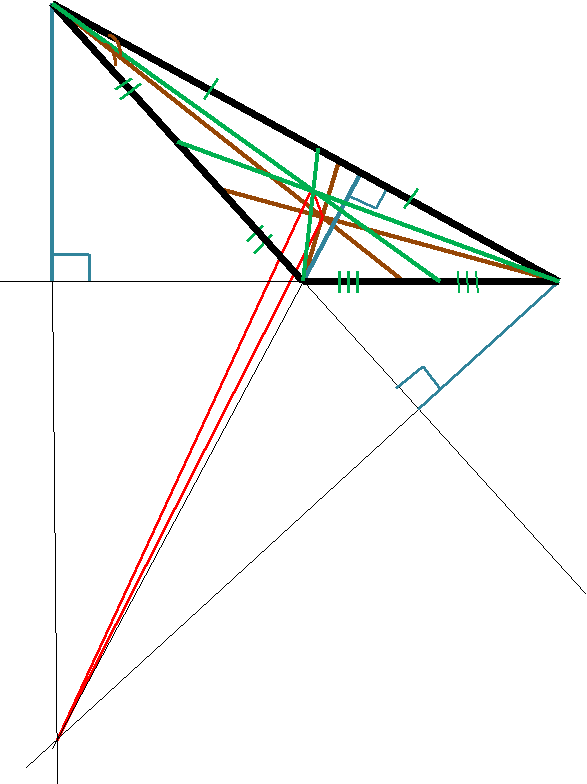 разностороннем тупоугольном треугольнике точки пересечения медиан, биссектрис и высот образуют треугольник АВС.
разностороннем тупоугольном треугольнике точки пересечения медиан, биссектрис и высот образуют треугольник АВС.
В
А
С
Использованная литература.
Учебник геометрии 7 – 9 классов Л. С. Атанасяна.
